Master of Arts
in
Geography
by
Tammy Renee Johnson
Committee in charge:
Professor Jeff
Dozier, Chairperson
Professor Joel
Michaelsen
Professor David
Hinkley
December 1998
INTRODUCTION
In California, almost all
precipitation occurs in the winter and spring months while the
summer and fall are dry.
Half of California’s water resources accumulate as snow and are
stored within the snowpack until it melts, usually beginning around
the first week of April.
With a system of reservoirs and aqueducts, snowmelt is routed
primarily to agricultural areas throughout the state in the summer,
when irrigation water is needed most.
This fresh water reserve system of natural and engineered
storage is potentially vulnerable to changes in climate.
In order to understand how water resources may be affected by
future changes, it is important to analyze how they have responded
to variations and changes in the 20th Century.
Climate research has revealed
changes that occur quickly, as if the system jumps past a threshold
and enters a different set of probable weather patterns.
One of these “steps” was discovered to have occurred
throughout the Pacific Ocean and the Americas in 1976 (Ebbesmeyer et
al., 1991). Time-series
analyses of 40 multidisciplinary variables, including oceanic,
atmospheric and biological data collected from 1968 to 1984,
indicated a consistent shift in 1976.
These results of fish catch, winds, El Niño Southern
Oscillation strength, chlorophyll, etc. were compared with a random
simulation to emphasize the certainty of this step.
About ten years ago, a
hydrologist at the Department of Water Resources (DWR), noticed that
the spring and early summer fraction of total annual eamflow had
been decreasing in the Sacramento area (Roos, 1991).
Correspondingly, a decrease in the April-July fraction was
reported across California (Wahl, 1991).
However, the total flows have not significantly changed in
these four main Northern California rivers.
Since these calculations were run on unimpaired streamflows,
the effects of dam building were removed.
Mr. Roos suggested that the cause could be a general trend
towards increased precipitation and warmer weather.
Historic weather records do show
that central California mountainous regions have undergone
significant warming during the last 50 years in January, February,
March, and June. The
winter surface-air temperatures have increased an estimated 2°C since a minimum near 1950
(ettinger and Cayan, 1995).
This warming has had a greater effect on streamflow from
lower elevation river basins than the higher ones (Dettinger and
Cayan, 1995). Further
studies investigating river runoff suggest that winter and early
spring streamflow have increased in the northern Sierra Nevada due
to higher temperatures and rain on snow events in lower elevations,
which cause earlier snowmelt (Pupacko, 1993).
While precipitation most strongly
influences treamflow at lower elevations, changes in Sierra Nevada
streamflow during May, June, and July, are influenced mostly by
temperature at elevations above 1000 meters (Aguado et al., 1992).
The highest streamflows are governed by the overall amount of
snow water equivalence (SWE) (Cayan et al., 1993).
General circulation model (GCM)
scenarios for an expected doubled-CO>2 climate in the next
several decades show greater warming in western North America in
winter, 4-6°C
(Mitchell et al., 1990).
Utilizing 3 GCMs, average California temperatures were predicted to
increase 3.8°C
while winter temperature increases averaged 3.5°C
and ranged from 1.3°C to 5.0°C
(Lettenmaier and Gan, 1990).
Along with elevated temperatures,
many climate models predict more precipitation, too.
The mountain climate response to these changes is that
snowpack will first increase with the additional precipitation.
However, this trend will reverse as higher temperatures raise
the snowline (Barry, 1990).
A site in the Sequoia National
Forest at 2813 meters above sea level was modeled using the
doubled-CO2 GCM outputs, coupled with an energy-based
snowmelt runoff model.
Predicted snowmelt runoff hydrograph changes ranged from 19 to 93
days earlier, depending on which temperature inputs were used.
The SWE is also estimated to dramatically decrease by 14% to
60%, with the snow season ending a month or two earlier (Tsuang and
Dracup, 1991) (Lettenmaier and Sheer, 1991).
Calculations also suggest increased winter flood risk, when
the reservoirs are already full (Lettenmaier and Gan, 1990).
Elevations below 2300 meters were most affected (Tsuang and
Dracup, 1991).
These findings suggest earlier snowmelt runoff and possibly
increased annual precipitation.
However, specific changes have been unclear since streamflow
integrates snow accumulation and melt throughout the season and
across all elevations of entire river basins.
This research uses historical snow data collected at specific
sites on a monthly schedule to analyze these trends at a higher
spatial and temporal resolution.
Monthly Snow Course Data
The California cooperative snow
courses are designated, flat open areas a thousand feet in length.
Ten samples are collected along a transect and averaged to
provide one monthly measurement, usually several times a year until
the time of melt, which averages one week before April.
Cooperative se surveys provide SWE data for 393 snow
courses spanning 9°
latitude, 7°
longitude and 3450 meters in elevation (Figure 1) and are accessible
via the world wide web (http://snow.water.ca.gov/)
These stations are remotely located, away from developing
areas that may introduce uncertainties such as an urban heat island
effect. This is the
tendency for urban areas to maintain a higher nighttime temperature
minimum than the surrounding landscape
(Klein and Goodridge,
1994).
The first courses were measured
in 1910, and most contain over 50 years of monthly SWE and snow
density measurements, which were collected from zero to six times
per season. Most
stations were sampled at least four times per year, within a few
days from the first of February, March, April and May.
Many of these courses were
created and regularly sampled in the 1930's, with sampling
increasing steadily until more stations were added in the 1950's.
The courses were sampled with the
Mount Rose sampler by experienced samplers and field notes were
later checked for arithmetic errors.
The number of samples taken changed after 1940, when 10
samples were averaged instead of the former 25 per course. Moved
courses were usually assigned a new station number, although some
stations are suspect.
Although these measurements are
of exceptionally high quality, these data present several challenges
for climate analyses because they were collected for water resources
management and were not consistent from year to year.
The average day that monthly sampling was conducted changed
by 3.2 days over the time series, occurring earlier in recent years.
Furthermore, stations were added and removed throughout the
years and these newer stations were not evenly distributed by
elevation, which accounts for about 6% of the SWE variability
(, 1990).
METHODS
Data Reduction
All available snow
course data through the 1996/1997 water year were downloaded from
the DWR web page. This
file included 51,168 SWE and depth measurements for 394 stations,
representing 18,298 station-years with data.
Of these data, one measurement was discarded because its SWE
value was 800 inches, an obvious error.
Thirteen additional observations were eliminated because they
had impossible densities, as calculated from the SWE and depth
measurements. This left
51,154 observations with the same number of stations and
station-years as before.
Discontinuous Stations
To identify possibly
altered stations, I generally followed a procedure for detecting
discontinuities in historic temperature data (erling and
Peterson, 1995). First,
each station’s measurements were normalized to account for differing
elevations, which is most responsible for snow variability after
overall seasonal wetness.
Stations were then grouped by river basins and elevation bins
with at least 5 nearby, highly correlated reference stations.
Group averages were subtracted from station data and the
differences were plotted in a time series to find discontinuities.
These normalized differences from group means were then
checked for sudden changes, which indicate possible alterations to a
particular station. Calculating means before and after every
station-year, and subtracting the difference did this. Every
station had a number for every year with data, which represented any
changes in the data before and after that year for that station.
Large positive or negative differences pointed to possible station
discontinuities. The first and last 10 years with data were
not considered in the difference of before and after means analyses
because of edge effects.
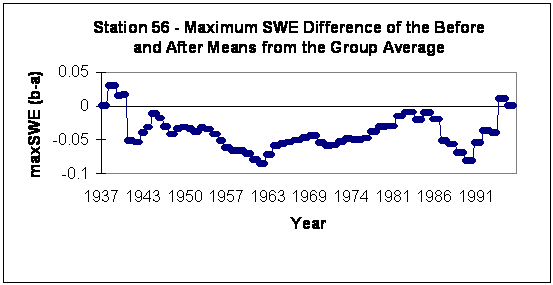
Figure 2
Potential problem
stations were defined to have trending differences that also
exhibited extreme difference of the mean values. Station 56 is the
most obvious example of the 33 stations removed that there could be
a discontinuity, in this case near 1962 (see Figure 2).
All stations with trending mean differences also contained
years that were two standard deviations from the mean.
These stations, although most likely unmodified, were
discarded to err on the side of caution.
These eliminated data are distributed throughout the range,
at all elevation bins and trend positively from the mean about as
often as negatively. The
remaining 361 stations cover 45,237 station measurements, which is
88% of the original data.
Climate Criterion
The next criteria for inclusion in the analysis were a minimum
30-year range with at least 10 observation years. This dataset
included 37,520 observations for 260 stations representing 14,151
station years.
Monthly Dataset
Like the previous requirement, the dataset for monthly analyses
required a minimum 30-year record with at least 10 years with
observations for a given month. In addition to this, at least
3 years per decade for each month were required. This resulted
in 33,941 observations for 259 stations and 808 station-months.
January and June were omitted due
to sparse data. This
left 33,215 observations for 259 stations covering 782
station-months (see Figure 1).
The resulting monthly data distribution, including January
and June, is given in table 1.
Observation Characteristics by Month
|
|
Jan
|
Feb
|
Mar
|
Apr
|
May
|
Jun
|
|
Obs
|
700
|
7733
|
7351
|
13,574
|
4383
|
26
|
|
Range
|
81
|
76
|
80
|
88
|
81
|
52
|
|
Stations
|
25
|
191
|
188
|
259
|
144
|
1
|
|
% Complete
|
67%
|
84%
|
80%
|
98%
|
78%
|
50%
|
Table 1
Station-Year Maximum Dataset
To determine station-year maximum SWE values and timing, I reduced
the monthly dataset in the following ways: stations were selected
for time series analyses that had at least 3 measurements per year
and 10+ years of measurements covering 30+ years.
These data also had to meet the following quality assurance:
the day of maximum SWE was not simply the last day measured unless
that month was the average month of melt and it was an
average-to-wet year.
This criterion discouraged false snowmelt timing calculations due to
sampling bias, yet accounted for precipitation variability and
associated snowmelt fluctuations.
Seasonal maximum SWE and the month of maximum SWE were computed for
each station, then these values were normalized by dividing yearly
amounts by station averages.
This resulting wetness factor can be compared to other
stations in various latitudes and elevations with different SWE
levels. Where a
station-year’s maximum SWE occurred in more than one month, the
later month was selected as the timing of melt.
Maximum Dataset Quality Assurance
Whereas the monthly dataset quality assurance was fairly
straightforward, the time of maximum SWE dataset was much more
difficult to substantiate. I felt that it was important to
distinguish any possible snowmelt timing and maximum accumulation
trends, since snowmelt timing is predicted to change so drastically
in a doubled carbon dioxide atmosphere.
Usually four monthly
sampling days were used to determine a time of maximum snow
accumulation and an amount.
The effect of monthly sampling on a regression analysis of
trends in date of maximum accumulation had to be determined, and
trends in sample dates further complicated the analysis.
However, a trending sample time cast further doubt as to the
validity of these results.
Fortunately,
extensive snow sensor and precipitation measurements in the Sierra
Nevada led to three different methods to verify that these trends
were meaningful. About
100 daily snow sensor stations have measurements spanning a couple
of decades. This was
useful in two ways.
First, 47 of these stations are located adjacent to snow course
stations so comparisons can be made for yearly maximum SWE and
monthly estimates.
Second, the effect of trends in sample dates can be calculated by
comparing the real maximums, as recorded by the daily instruments,
with any other results generated by sub-sampling this daily dataset.
With these data I compared various sample days’ (in time from
the first-of-the-month) effects on the month of maximum SWE
determination.
The third test, which also determined the effect of a
trending sample day, was to compare DWR first-of-the-month corrected
SWE values with the original SWE measurements.
These are data based on the measurements but corrected to
what the SWE probably would have been on the first of the month.
Adjusted SWE is calculated by multiplying precipitation
between the sample day and the first by a correction factor.
Adjusted SWE = measured SWE *
precipitation * correction factor
Precipitation is positive if the day sampled is before the
first.
Correction factors are unique for each snow-rain station
pairing.
Sampled Station Bias
Analyses were
separated into 100 meter elevation bins to both diminish station
sampling bias and to exploit the spatial snow course clarity that is
missing from the river data.
Daily Snow Sensor Experiment
I used the daily snow sensor data
to determine the effects of a trending sampling schedule on the
time-series regressions.
With daily data, I could create monthly datasets with various
sampling schedules to check the effects of earlier sampling.
However, first I quality checked the sensor data and found
that it contained many obvious errors.
I rejected the obviously erroneous data and ran a cubic
spline interpolation to fill in the missing daily data.
A cubic spline is a segmented function consisting of
third-degree polynomial functions joined together so that the whole
curve and its first and second derivatives are continuous.
Missing dates were filled-in with the appropriate spline
function.
Using validated daily sensor data, actual seasonal maximum SWE and
the month of maximum SWE was calculated for each station. Then
these real values were compared to sensor estimates using only
monthly sampling to check the effects of monthly sampling.
Finally, errors were calculated for both maximum SWE and the month
of maximum SWE and fit to the number of days of earlier or later
sampling. These errors associated with the 15 days before and
after the real maximum first-of-the-month measurement were used to
calculate the effect of the earlier sample timing.
I considered each day in the real
maximum SWE month as the monthly sample day.
This value was compared to the remaining monthly
measurements, which were first-of-the-month values.
This represented a perfect monthly dataset with the exception
of one month off by a set number of days.
The SWE value for any day was compared to the next highest,
first-of-the-month, monthly SWE value to decide which of those two
measurements would be classified as the maximum SWE value and month.
The error associated with a given number of days from the
first could then be calculated by subtracting its results with the
actual maximum SWE and month of maximum SWE values. The
differences were fitted with the number of days from the first to
determine the error due to an inconsistent sampling schedule.
For example, daily snow sensor
SWE data, dates and station information were run through a program
to calculate these numbers listed in Table 2 for station 162 in May
1991. Station 162 is on
the east side of the Sierra Nevada, in the Tuolumne river basin at
2562 meters above sea level.
The second highest first-of-the-month SWE value is 26.6
inches and occurs in April.
The actual highest measurement recorded is 27.0, which is
recorded in the table with the 2nd day before the first (April 30th).
Example of Sampling Effects Calculations
|
SWE
|
Days
to the First
(neg.
= prev. month)
|
Different SWE
(less
than actual)
|
Different Month
(pos.
= false early)
|
|
24.2
|
-14
|
0.4
|
1
|
|
23.9
|
-13
|
0.4
|
1
|
|
23.6
|
-12
|
0.4
|
1
|
|
23
|
-11
|
0.4
|
1
|
|
22.8
|
-10
|
0.4
|
1
|
|
23
|
-9
|
0.4
|
1
|
|
22.9
|
-8
|
0.4
|
1
|
|
23.8
|
-7
|
0.4
|
1
|
|
24.8
|
-6
|
0.4
|
1
|
|
25.6
|
-5
|
0.4
|
1
|
|
24.9
|
-4
|
0.4
|
1
|
|
25
|
-3
|
0.4
|
1
|
|
25.2
|
-2
|
0.4
|
1
|
|
25
|
-1
|
0.4
|
1
|
|
26.8
|
0
|
0.2
|
0
|
|
26.6
|
1
|
0.4
|
0
|
|
27
|
2
|
0.4
|
0
|
|
25
|
3
|
0.4
|
1
|
|
25.6
|
4
|
0.4
|
1
|
|
26.5
|
5
|
0.4
|
1
|
|
27
|
6
|
0
|
0
|
|
26.6
|
7
|
0.4
|
0
|
|
25.9
|
8
|
0.4
|
1
|
|
26.8
|
9
|
0.2
|
0
|
|
26.6
|
10
|
0.4
|
0
|
|
26.8
|
11
|
0.2
|
0
|
|
26.6
|
12
|
0.4
|
0
|
|
26.2
|
13
|
0.4
|
1
|
|
26.4
|
14
|
0.4
|
1
|
|
26.6
|
15
|
0.4
|
0
|
|
26.6
|
16
|
0.4
|
0
|
Table 2
The following explains the
program that calculated the error, or difference values.
It was not used to adjust any results, but only to indicate
potential errors due to the sampling scheme.
The first step in the process was
to filter the daily data and interpolate missing values.
The day of the month and the month numbers were pulled out of
the date, and these numbers were grouped so that all measurements
after the 15th of the month are grouped with the
following month. Years
are also adjusted to water years in this way. The days until the
first-of-the-month are then calculated.
I accounted for varying monthly length but I didn’t calculate
exact February leap year days, so February 29th readings
will appear to be on the first of March.
Then I simulate perfect monthly
sampling by pulling all SWE values on the first of each month.
The highest monthly SWE value and month are then stored.
To compare the errors associated with various sample days,
the next highest first-of-the-month measurements and months are also
recorded. Finally, the
actual highest daily SWE measurements for each station-year are
recorded.
The resulting error in maximum
SWE is the difference between the actual highest SWE value and the
monthly measurement. The
monthly SWE used is either the maximum month daily SWE amount (the
one being tested for timing effects) or the second highest
first-of-the-month maximum SWE value (whichever is highest).
All of these results are positive or zero, indicating how
much lower the SWE result is from the real maximum SWE.
Sampling effects on snowmelt
timing were calculated similarly.
The month of snowmelt timing error was called zero if the
given daily SWE measurement was higher than the second highest
first-of-the-month SWE measurement.
In this case a measurement was as accurate as the “perfect”
one for determining the timing of maximum SWE, despite when it was
collected. However, if
the SWE value dropped below the next highest monthly sample value,
it was inaccurate. The
error was determined by how many months the result was off.
I subtracted the second month from the real maximum SWE
month, so positive numbers indicate false earlier melt.
The errors were fit to the number
of days from the first-of-the-month to calculate the maximum SWE and
month of maximum SWE change as the sample time changes.
All station-years were used to calculate average sample
timing effects.
Climate Changes
Climate cycles or
steps were checked by a method similar to the discontinuous station
procedure, but instead of taking differences from means of yearly
group averages, each station's standardized wetness was analyzed.
Calculating means before and after every station-year, and
subtracting the difference did this.
The first and last 10
years with data are not considered in the difference of before and
after means analyses because of severe edge effects.
Very high or very low differences indicate climate change.
Time-Series Regressions
All station
measurements were standardized to station means to account for
changing station elevations with time.
Estimated slopes were further standardized to changes per 50
years for comparison.
Percent changes and absolute changes were computed for monthly,
maximum and the timing of maximum for river basins above and below
2400m and 100-meter elevation bins.
River basin changes are mapped throughout the Sierra Nevada
and elevation bin changes are plotted.
RESULTS
Sample Timing Effects
Monthly sample timing has very little effect on
measured maximum SWE.
The average bias is a 0.3% reduction per day sampled after the
first. The monthly
sampled maximum will always be either less than or equal to the true
maximum. However, there
is a greater effect on the calculated timing of maximum SWE.
Monthly sampling and earlier sample timing cause a false
later maximum SWE timing change of 0.8 days over the 50-year period.
When broken into elevation bins, the greatest schedule change
of 7.2 days amounts to a false later melt of 2.1 days.
Although 80% of the monthly sample days identify the correct
maximum SWE month, monthly sampling creates melt-timing errors with
3.4 times more erroneous earlier melt months than false later ones.
An examination of the sample data indicates
that on the first-of-the-month with maximum SWE, the sampling error
indicates false earlier melt. The snow is actually melting
later. This is probably because the SWE levels tend to drop
faster than they accumulate throughout the season. The result
is that monthly measurements are more likely to catch the upside
(earlier) rather than the steeper downside. Earlier sampling
appears to be catching more times near this peak.
These slight changes were not corrected in the
analyses. Instead,
results staying within 5% of the maximum SWE and within 2 days per
50 years for snowmelt timing were considered to be unchanged.
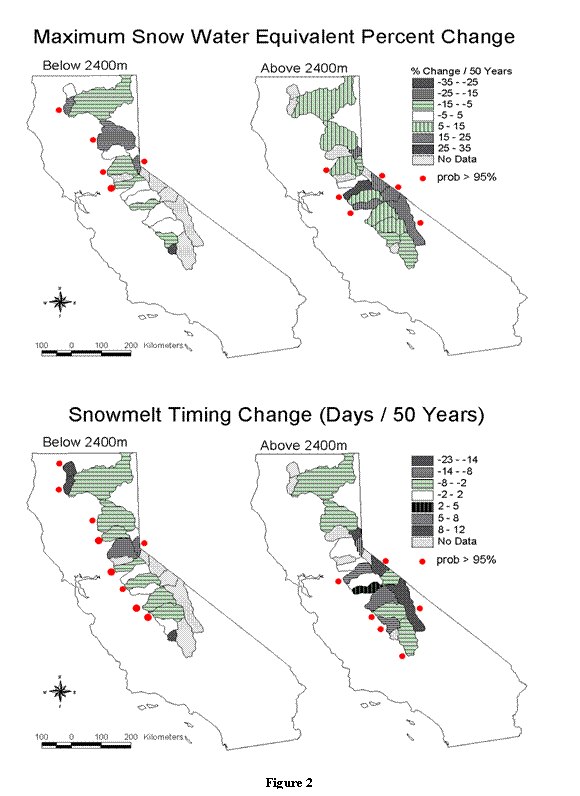
River Basin Trends
Regressions on time of station data from individual river basins
below 2400 meters consistently indicate less maximum SWE or no
change (Figure 2).
Downward maximum SWE trends of 5% to 25% per 50 years are supported
by 95% confidence in the Trinity, Feather, Lake Tahoe, American and
Mokelumne basins. The
Tule’s estimated change of 33% less SWE per 50 years lacks
confidence because there is only one station that survived the data
quality filters. It has
31 observations.
Above 2400 meters, most river basins show upward maximum SWE trends.
The southern east-draining Walker, Mono Lake and Owens basins
all show significant maximum SWE increases of 15% to 25%.
The west-draining American, Stanislaus and Merced also
indicate more snow accumulation.
Snowmelt timing changes in the lower elevations consistently
indicate earlier melt or no change.
Nine of the 15 basins’ trends are supported with 95%
confidence. The Scott
and Trinity River basins in the northwestern corner are melting two
and three weeks earlier, respectively
At higher elevations, snowmelt has also tended to occur earlier,
with six basins showing a clear change in the time of maximum snow
accumulation. Only one
of these indicated later melt, the east-draining Owens, which is
estimated to be melting a week and a half later than it did 50 years
ago.
Monthly estimated changes for the basins are summarized in Table 3
and all estimates supported by 95% confidence are in bold.
The basins are arranged by latitude, with the west-draining
basins listed first, followed by the east-draining results.
All 15 lower elevation, monthly basin trends with strong
statistical confidence indicate decreasing SWE levels.
Of the six higher elevation estimates with good confidence,
four suggest increasing SWE trends.
Three of these basins are located on the east-draining side
of the range.
|
|
Monthly Snow Water
Equivalent Estimated Percent Change Per 50 Years
|
|
|
Below 2400 meters
|
Above 2400 meters
|
|
Basin
|
Feb
|
Mar
|
Apr
|
May
|
Feb
|
Mar
|
Apr
|
May
|
|
Scott
|
-2.3
|
-15.5
|
-32.2
|
-16.2
|
|
|
|
|
|
Trinity
|
-24.3
|
-38.1
|
-14.9
|
-31.1
|
|
|
|
|
|
Yuba
|
-1.6
|
-3.3
|
0.5
|
-10.3
|
|
|
|
|
|
American
|
-16.4
|
-15.7
|
-17.5
|
-18.1
|
16.1
|
11.7
|
8.4
|
2
|
|
Mokelumne
|
-16.1
|
-13.7
|
-17.9
|
-7.5
|
0.6
|
-5.7
|
-1
|
-2.6
|
|
Stanislaus
|
6.3
|
-4
|
-8.2
|
7.1
|
41.7
|
38.6
|
3.7
|
27.4
|
|
Tuolumne
|
31.1
|
0.6
|
-19.5
|
|
21.3
|
3.9
|
6.7
|
20.1
|
|
Merced
|
-8.8
|
-11.2
|
-12.4
|
-7.3
|
28
|
-3
|
8
|
20.6
|
|
San Joaquin
|
7.1
|
2.9
|
6.1
|
-3
|
6.3
|
10.8
|
11.5
|
-2.4
|
|
Kings
|
-2.6
|
-12.7
|
-9.7
|
22.9
|
14
|
15.4
|
8.6
|
-34.4
|
|
Kaweah
|
-20.2
|
-19.9
|
-17.8
|
-26.5
|
-43.4
|
19.2
|
2.5
|
-47
|
|
Tule
|
-14.4
|
-8.2
|
-36
|
|
|
|
|
|
|
Kern
|
-5
|
|
-20
|
|
-19.3
|
10.7
|
10.3
|
-36.6
|
|
|
|
|
|
|
|
|
|
|
|
Sacramento
|
-19.2
|
-17.3
|
-3.5
|
-16
|
13.9
|
7.6
|
12.7
|
13.9
|
|
Feather
|
-9
|
-13.1
|
-7.6
|
-20.2
|
5.8
|
-5.6
|
2.7
|
4.3
|
|
Truckee
|
-35.4
|
-20.4
|
0.6
|
-1.6
|
10.7
|
15.1
|
9.9
|
26.5
|
|
Lake Tahoe
|
-19.4
|
-19.2
|
-8
|
-53.8
|
-1.5
|
-3.2
|
6.2
|
7.7
|
|
Carson
|
|
|
|
|
|
|
-0.5
|
|
|
Walker
|
|
|
32.4
|
|
26.3
|
22.8
|
13.3
|
34.3
|
|
Mono Lake
|
|
|
|
|
5.6
|
17.7
|
25.2
|
|
|
Owens
|
|
|
|
|
-8.9
|
16.5
|
14
|
11
|
When analyzed by 100-meter elevation bins, the reason for breaking
river basin analyses up into groups above and below 2400 meters
becomes more apparent.
There is a clear elevational component to the observed snow
accumulation trends.
Throughout the Sierra Nevada, snow courses below 2400 meters have
lost 14% of their maximum SWE while higher ones have gained 8%.
Figure 3 clearly shows a strong elevational component affecting the
trends in maximum SWE.
The snowmelt timing graph does not exhibit a strong linear
relationship through the higher elevation bins, but there is
obviously earlier melt in the lower elevations.
Half of the lowest elevation bins’ trends are supported with
95% confidence.
At lower elevations, February through May show increasingly less SWE
(Table 4). At the higher
elevations, February looks unchanged.
By March 1st, The higher elevations have gained
18% more snow. This
extra snow per 50 years remains through April then decreases in May.
(The May graph is broken because an elevation bin lacked
sufficient data to run the time-series regression.)